QAOA Implementation for MAX-SAT Problems

Christian Neureuter

Completed work

Quantum Engineer

Scientist

Software Engineer

Python

Computer Software

QAOA for MAX-SAT Problems

A comprehensive Python implementation of the Quantum Approximate Optimization Algorithm (QAOA) for solving MAX-SAT problems including Max-Cut and MAX 3-SAT using Google's Cirq quantum computing framework.

A deep dive into hybrid quantum-classical computing with a comprehensive implementation of the Quantum Approximate Optimization Algorithm (QAOA) to solve NP-hard combinatorial optimization problems. This project tackles multiple variants of the Maximum Satisfiability (MAX-SAT) problem, including Max-Cut on ring graphs (MAX-2-SAT) and general MAX-3-SAT with arbitrary boolean clauses. The implementation features a robust pipeline built with Python and Google's Cirq framework. It constructs parameterized quantum circuits that encode problem Hamiltonians, using standard ZZ gates for Max-Cut and novel, custom-built 3-qubit gates for the more complex MAX-3-SAT instances. A classical Nelder-Mead optimizer iteratively refines the circuit parameters to navigate the solution space and find high-quality approximate solutions. The project includes extensive performance analysis, calculating approximation ratios by benchmarking QAOA results against a classical brute-force solver and demonstrating performance scaling with increased circuit depth.

TECHNOLOGIES USED

Python • Google Cirq

KEY METRICS

2 NP-Hard Problem Classes Solved

90%+ Approximation Ratios Achieved

Project Overview

This project demonstrates a complete implementation of QAOA, a hybrid quantum-classical algorithm that combines quantum circuits with classical optimization to solve combinatorial optimization problems. The implementation covers multiple MAX-SAT problem variants including:

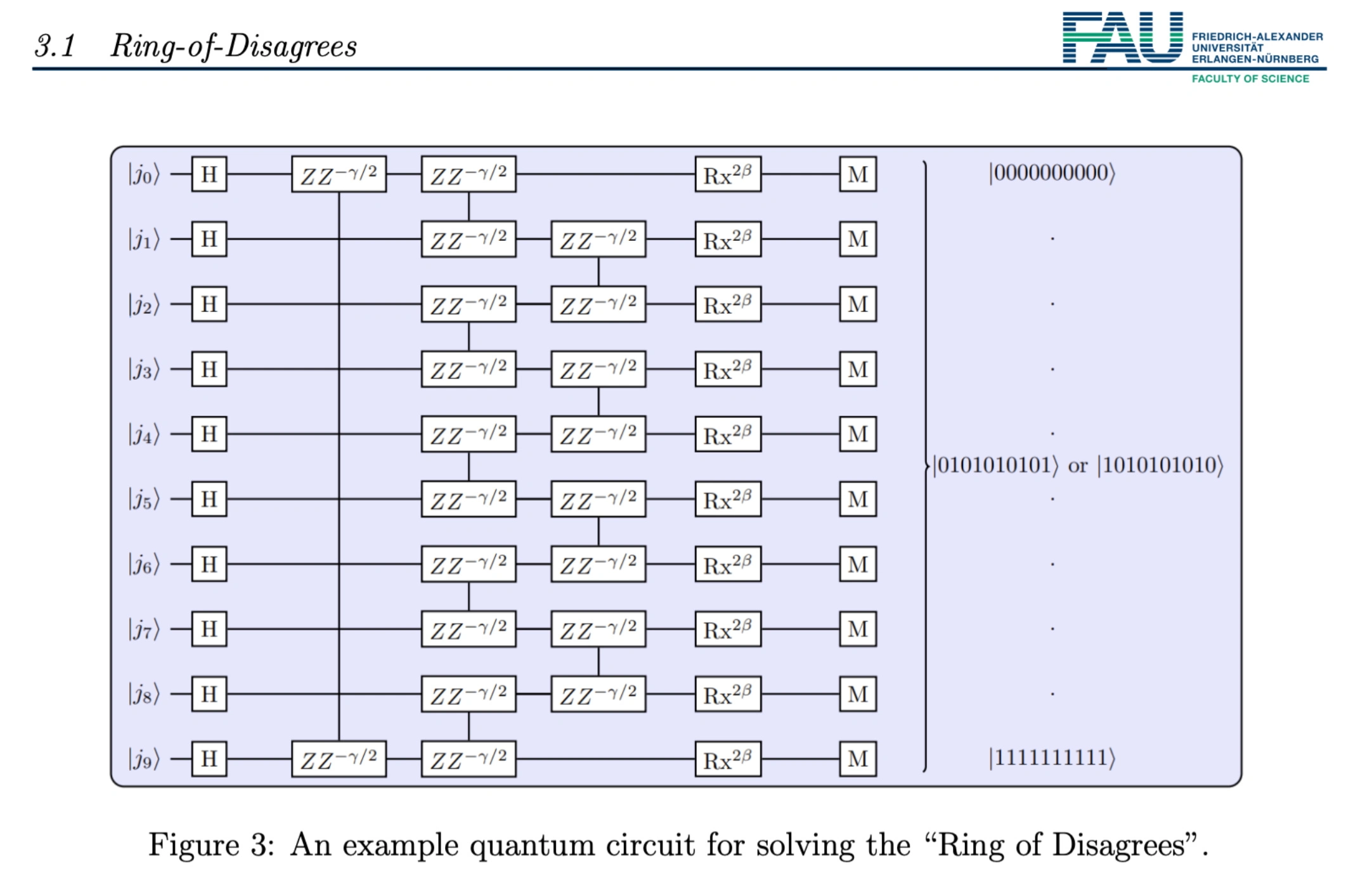
MAX 2-SAT (Ring of Disagrees): Max-Cut problem on ring graphs

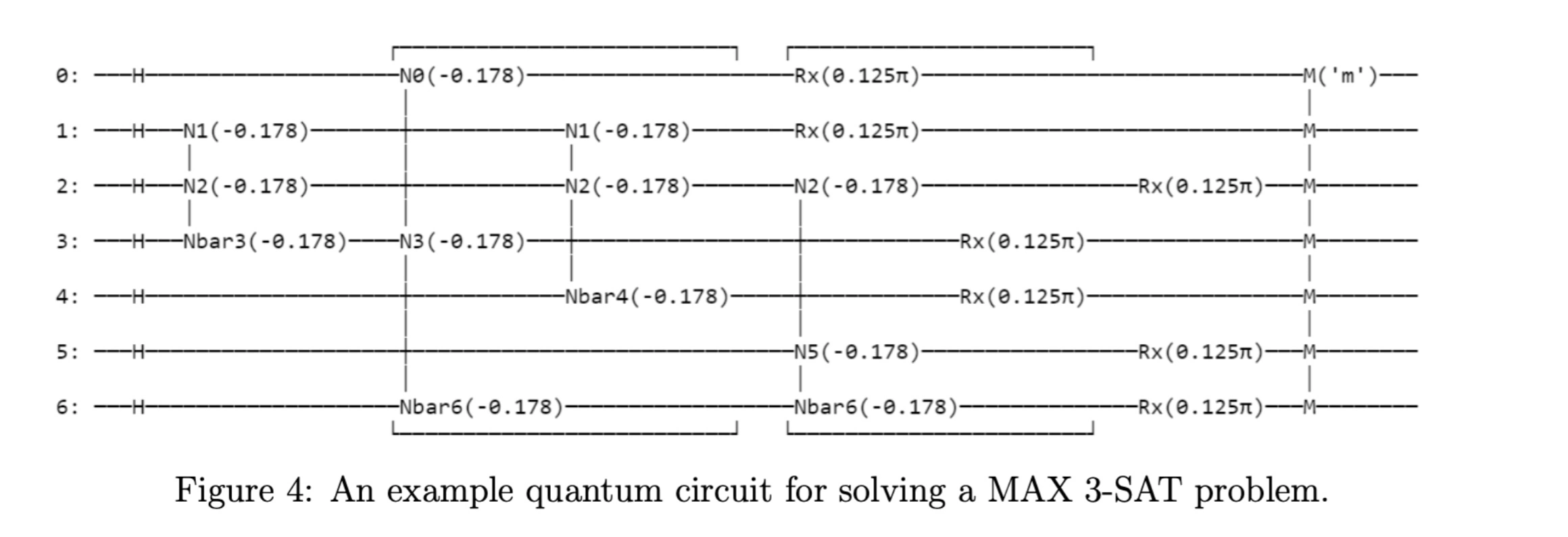
MAX 3-SAT: General 3-satisfiability problems with arbitrary boolean clauses

What is QAOA?

QAOA (Quantum Approximate Optimization Algorithm) is a variational quantum algorithm that:

Uses parameterized quantum circuits to prepare quantum states

Employs classical optimization to find optimal parameters

Provides approximate solutions to NP-hard combinatorial problems

Demonstrates potential quantum computational advantages

MAX-SAT Problems

This implementation addresses multiple SAT problem variants:

MAX 2-SAT (Ring of Disagrees):

Finding optimal vertex partitions to maximize disagreeing edges

Ring graph topology with neighboring vertex interactions

Cost function: C ( z ) = ∑ ⟨ j k ⟩ 1 2 ( 1 − σ j z σ k z )

MAX 3-SAT:

General satisfiability problems with 3-literal clauses

Arbitrary boolean clause structures

Custom 3-qubit gates for clause evaluation

Cost function: C ( z ) = ∑ i j k z i z j z k (with possible negations)

Applications: Network design, VLSI circuit design, clustering, constraint satisfaction, and combinatorial optimization

Project Structure

QAOA/
├── README.md                           # This file
├── LICENSE                            # MIT License
├── requirements.txt                   # Python dependencies
├── .gitignore                        # Git ignore patterns
├── notebooks/                        # Jupyter notebooks
│   ├── qaoa-max-sat-implementation.ipynb  # Complete QAOA implementation & analysis
│   ├── qaoa-code-presentation.ipynb       # Clean presentation version
│   ├── qaoa-presentation.ipynb            # Academic presentation notebook
│   └── qaoa-presentation.slides.html      # HTML slide deck
└── docs/                            # Documentation
    ├── algorithm_explanation.md      # Detailed algorithm explanation
    └── QAOA_for_MAX_SAT.pdf         # Academic research paper

Getting Started

Prerequisites

Python 3.7+

Jupyter Notebook

pip or conda

Installation

Clone the repository:

git clone https://github.com/cneureuter/qaoa-max-sat.git
cd qaoa-max-sat

Install dependencies:

pip install -r requirements.txt

Launch Jupyter:

jupyter notebook

Open and run notebooks/qaoa-max-sat-implementation.ipynb

Key Features

Complete QAOA Implementation

Parameterized quantum circuits using Cirq

ZZ gates for MAX 2-SAT (Ring of Disagrees) problems

Custom 3-qubit gates for MAX 3-SAT problems

Rx gates for mixing Hamiltonian

Multiple Problem Formulations

MAX 2-SAT implementation with ring topology

MAX 3-SAT implementation with arbitrary clauses

Proper operator construction for different eigenvalue requirements

Classical Optimization

Nelder-Mead optimization for parameter tuning

Performance tracking and analysis across problem types

Comprehensive Analysis

Circuit depth performance comparison

Approximation ratio calculations

Brute-force optimal solution verification

Statistical analysis of solution distributions

Professional Visualization

Circuit diagrams for different problem types

Performance plots and probability distributions

Clear documentation and explanations

Algorithm Details

Circuit Structure

The QAOA circuit consists of:

Initialization: Hadamard gates create uniform superposition

Problem Layers:

ZZ gates for MAX 2-SAT encoding

Custom 3-qubit gates for MAX 3-SAT encoding

Mixing Layers: Rx gates provide transitions between states

Measurement: Final measurement in computational basis

Mathematical Foundation

MAX 2-SAT (Ring of Disagrees):

Problem Hamiltonian: H C = ∑ ⟨ j k ⟩ 1 − Z j Z k 2

Uses Pauli-Z operators with eigenvalues {+1, -1}

MAX 3-SAT:

Problem Hamiltonian: H C = ∑ i j k z ^ i z ^ j z ^ k

Custom operators: z ^ = 1 2 ( 1 ± σ z ) with eigenvalues {0, 1}

Handles arbitrary 3-literal clause structures

Common Elements:

Mixing Hamiltonian: H M = ∑ i X i

QAOA State: | γ , β ⟩ = ∏ j = 1 p e − i β j H M e − i γ j H C | + ⟩ ⊗ n

Parameter Optimization

The algorithm optimizes two sets of parameters:

γ (gamma): Controls the strength of the problem Hamiltonian

β (beta): Controls the strength of the mixing Hamiltonian

Results

The implementation demonstrates:

Consistent high approximation ratios for both problem types

Performance scaling with increasing circuit depth (p=1,2,3)

Efficient classical optimization convergence

Verification against brute-force optimal solutions

Statistical analysis showing concentration around optimal values

Performance Highlights

Optimal Solutions: Consistently finds optimal solutions for small instances (n≤10)

Problem Versatility: Successfully handles both MAX 2-SAT and MAX 3-SAT formulations

Scalability: Demonstrates performance across different circuit depths

Accuracy: High approximation ratios achieved through parameter optimization

Educational Value: Complete implementation suitable for learning QAOA concepts

Usage Example

# Core QAOA implementation is in the Jupyter notebooks
# Key functions include:

def qaoa_max_sat_circuit(qubits, betas, gammas, clauses, problem_type):
    """Constructs the complete QAOA circuit for MAX-SAT problems"""
    # Implementation in notebooks/qaoa-max-sat-implementation.ipynb

def evaluate_sat_cost(bitstrings_df, clauses, problem_type):
    """Evaluates cost values from measurement results"""
    # Implementation in notebooks/qaoa-max-sat-implementation.ipynb

# Supports both MAX 2-SAT and MAX 3-SAT problem types

Contributing

This project welcomes contributions! Areas for enhancement:

Hardware-specific circuit optimizations

Additional SAT problem variants (MAX k-SAT for k>3)

Performance improvements and error mitigation

Extended documentation and tutorials

Quantum error correction integration

References

Farhi, E., Goldstone, J., & Gutmann, S. (2014). A quantum approximate optimization algorithm. arXiv:1411.4028

Google Cirq Documentation: https://quantumai.google/cirq

NetworkX Documentation: https://networkx.org/

Academic Paper: QAOA_for_MAX_SAT.pdf (included in docs/)

License

This project is licensed under the MIT License - see the LICENSE file for details.

Academic Context

This project was developed as part of advanced quantum computing coursework at FAU Erlangen-Nuremberg under supervision of Professor Michael Hartmann, demonstrating:

Practical implementation of variational quantum algorithms

Integration of quantum and classical computing paradigms

Performance analysis and optimization techniques

Academic rigor in algorithm development and testing

Professional documentation and presentation skills