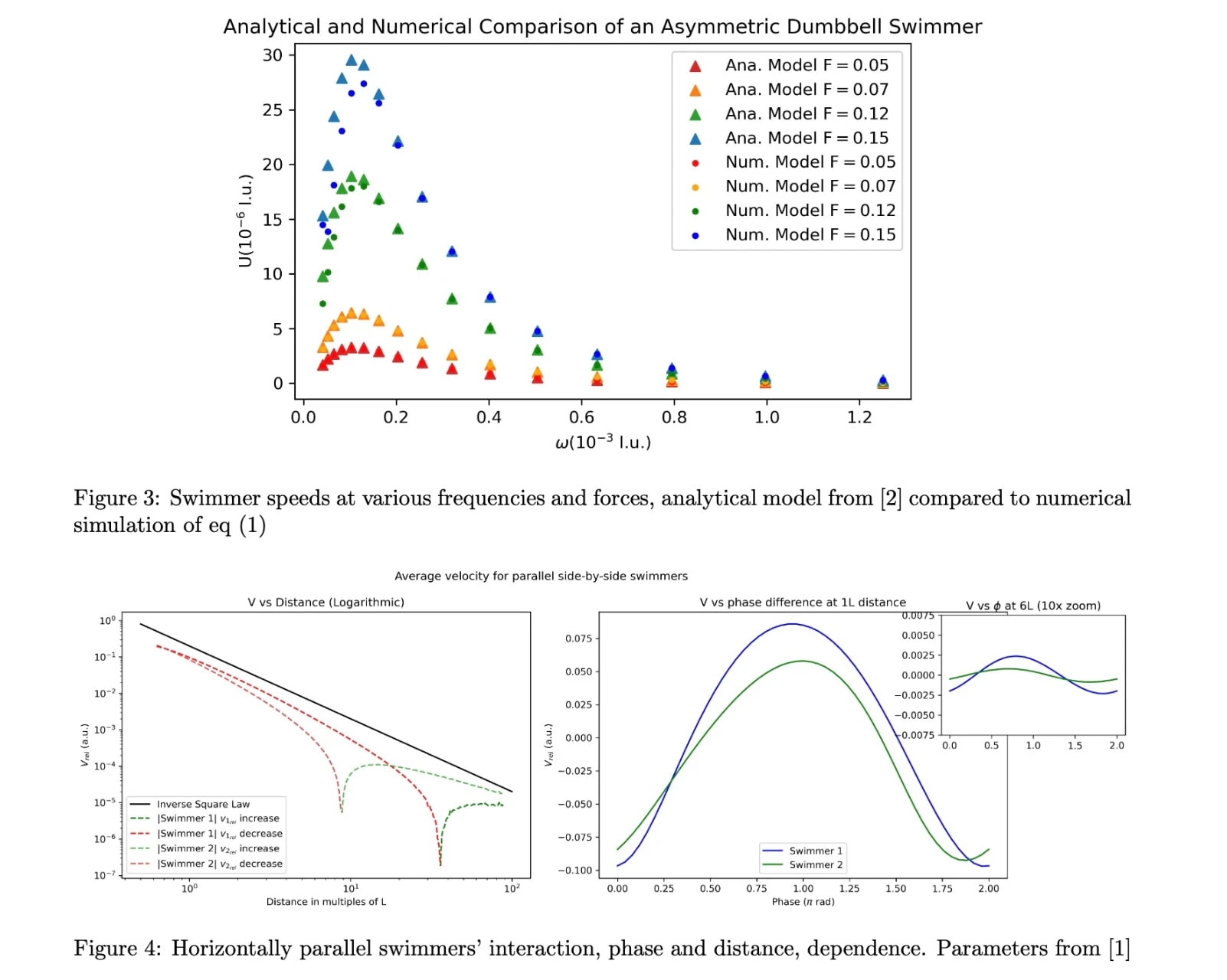
This project explores the fascinating world of mesoscale swimmers, specifically focusing on how their interactions are influenced by mass, distance, and configuration. Using a "dumbbell swimmer" model—two beads of different masses connected by a spring—this work investigates the hydrodynamic forces that govern locomotion in the regime between microscopic and macroscopic scales.

At the microscale, viscous forces dominate over inertial forces, a realm defined by a low Reynolds number. In this environment, reciprocal motion (like a scallop opening and closing) results in no net movement. This principle is known as the Scallop Theorem.

This project investigates swimmers in the "mesoscale," where inertia is not entirely negligible. By giving the two beads of the dumbbell swimmer different masses, we introduce an asymmetry. This asymmetry breaks the time-reversal symmetry of the stroke, allowing the swimmer to achieve net locomotion even with a simple, reciprocal driving force.

The interactions between swimmers are modeled using the Oseen tensor, which serves as an approximation of the hydrodynamic interactions at low Reynolds numbers. This allows for the study of how the flow field generated by one swimmer affects its neighbors.

This repository is organized into several directories:

mathematica_notebooks/: Contains the core simulations and analyses performed in Wolfram Mathematica.

jupyter_notebooks/: Contains supplementary analyses and plotting performed in Python.

docs/: Contains project documentation including the final report, presentation slides, and reference materials.

data/: Intended for raw data files.

plots/: Intended for generated plots and figures.

1D_Swimmer_Verification.nb: Verifies the 1D single swimmer model against analytical results.

1D_to_2D_Comparison.nb: Extends the model from 1D to 2D and confirms consistency.

2D_Single_Swimmer.nb: A clean implementation of a single swimmer in a 2D environment.

2D_Two_Swimmers_Base.nb: Implements the base model for two interacting swimmers in 2D.

2D_Two_Swimmers_Interaction_Analysis.nb: Analyzes the interaction between two swimmers as a function of distance and phase.

Synergistic_Configuration_Analysis.nb: Investigates configurations and parameters that lead to constructive interference (increased speed).

Antagonistic_Configuration_Analysis.nb: Investigates configurations and parameters that lead to destructive interference (decreased speed).

Python_Swimmer_Model.ipynb: A Python implementation of the swimmer model.

Python_Data_Analysis.ipynb: Further analysis and visualization of the simulation data using Python.

The simulations revealed a rich set of interaction dynamics:

Distance Dependence: The interaction strength follows various power laws depending on the distance between swimmers, with a prominent inverse square dependence in the mid-range.

Phase & Configuration: The relative phase of the swimmers' strokes and their geometric configuration (e.g., parallel, perpendicular) are critical, determining whether the interaction is helpful (synergistic) or harmful (antagonistic).

Mass Amplifies Interaction: Increased mass does not simply increase a swimmer's speed but rather amplifies the strength of the interaction, whether it is positive or negative. In optimal setups, swimmers can more than septuple their speed, while in the worst cases, they can be brought to a near-complete stop.

Mathematica: The .nb files can be run using Wolfram Mathematica.

Jupyter: The .ipynb files require Python with libraries such as numpy, matplotlib, and jupyter.