Optimization of Microchannels for Joule Heating Control

Optimización de Microcanales con Geometrías de Postes para el Control del Calentamiento por Efecto Joule y la Concentración del Campo Eléctrico.docx

Bretón López Luis Andoni 1‡, Mares Serrano Ian Manuel 2‡ , Montero Aceves Carla3‡ , Baker Santana Andrich4‡

1 Escuela de Ingeniería y Ciencias, Tecnológico de Monterrey, Av. Eugenio Garza Sada 2501, 64849 Monterrey, Nuevo León, México

Keywords: Efecto Joule, Microfluídica, Corriente eléctrica, Temperatura, Resistencia

Abbreviations: DC-iEK, dispositivos electrocinéticos de corriente continua, PDMS, Polidimetilsiloxano, iEK, Electrocinética basada en aisladores

Abstract

La optimización de microcanales con geometrías de postes ofrece un enfoque favorable para el control del calentamiento por el Efecto Joule y la concentración del campo eléctrico en dispositivos microfluídicos, lo que es esencial para aplicaciones como diagnósticos biomédicos, análisis químicos, etc. En el presente estudio se abordan los desafíos del Efecto Joule, que se define a grandes rasgos como un fenómeno donde la corriente eléctrica genera calor en medios conductores, comprometiendo así el rendimiento y la estabilidad de los dispositivos.

A través de simulación en COMSOL Multiphysics, se investigó cómo las configuraciones de los postes elípticos tienen influencia en la distribución del campo eléctrico y el comportamiento térmico. Estas simulaciones se iniciaron con una referencia de voltaje de 2500 V, las cuales revelaron una generación considerable de calor en regiones de alta intensidad de campo alrededor de los postes. Seguidamente, un diseño optimizado redujo el voltaje operativo a 1500 V, logrando una mayor concentración del campo eléctrico sin intensificar el calor. Esto se llevó a cabo mediante la disposición intercalada de postes elípticos los cuales enfocan el campo en áreas específicas, haciendo esto se mitigan los gradientes de temperatura no deseados. Finalmente, el diseño optimizado equilibró la reducción de consumo energético con una gestión térmica mejor, manteniendo una dinámica de fluidos efectiva y una eficiente manipulación de partículas. Los resultados mostraron una reducción en la temperatura máxima del fluido y una intensidad de campo eléctrico de V/m bajo un voltaje reducido de 1500 V, validando así la eficacia del enfoque.

Introduction

La microfluídica se ha consolidado como una tecnología esencial para manipular y analizar fluidos a escalas extremadamente reducidas, con aplicaciones destacadas en biomedicina, química analítica y el desarrollo de dispositivos de diagnóstico. Su capacidad para llevar a cabo experimentos con volúmenes mínimos, alta precisión y costos operativos reducidos ha transformado la manera de abordar desafíos complejos en el ámbito científico y tecnológico [1-3]. Entre las diversas técnicas empleadas, los dispositivos electrocinéticos de corriente continua (DC-iEK) sobresalen por su habilidad para gestionar fluidos y campos eléctricos en canales confinados. Estos sistemas son particularmente valiosos en aplicaciones que requieren la separación y el control de moléculas o partículas según sus propiedades eléctricas. [4]

No obstante, la implementación de tecnologías microfluídicas enfrenta diversos retos, siendo uno de los más relevantes el calentamiento por efecto Joule, este fenómeno ocurre cuando un campo eléctrico aplicado genera calor en un medio conductor debido al flujo de corriente eléctrica. Esto puede comprometer la estabilidad térmica de los dispositivos y afectar el rendimiento de las operaciones microfluídicas. El incremento de la temperatura puede modificar las propiedades fisicoquímicas de los fluidos, provocar gradientes térmicos no deseados e incluso dañar los materiales que conforman los canales [5,6]. Por esta razón, es importante comprender el efecto Joule para el diseño óptimo de dispositivos DC-iEK.

En los dispositivos DC-iEK, el calor generado por el efecto Joule está estrechamente relacionado a la intensidad del campo eléctrico aplicado. En zonas donde el campo eléctrico es más intenso, se produce una mayor generación de calor [7]. Este efecto se vuelve especialmente importante en dispositivos con geometrías complejas, como microcanales que contienen postes o barreras, ya que estas estructuras perturban el campo eléctrico, intensificando sus variaciones y concentrando el calentamiento en áreas específicas [8]. Esto plantea desafíos adicionales en el diseño y manejo térmico de estos sistemas [9].

Los modelos computacionales se han convertido en herramientas fundamentales para enfrentar estos desafíos. El software COMSOL Multiphysics destaca por su capacidad para simular con detalle el comportamiento eléctrico y térmico en dispositivos microfluídicos. Este programa resuelve ecuaciones acopladas, como la ecuación de Laplace para describir el campo eléctrico y la ecuación de transferencia de calor para modelar la distribución térmica [8], permitiendo predecir fenómenos clave y estudiar el efecto de diferentes diseños geométricos y condiciones de operación. Estas simulaciones ofrecen una perspectiva integral para optimizar el diseño de dispositivos, reduciendo los costos asociados a los experimentos.

Este estudio se centra en la optimización de un microcanal con geometrías de postes diseñadas específicamente para mitigar el calentamiento generado por el efecto Joule, sin comprometer la intensidad de campo eléctrico. A través de simulaciones en COMSOL, se examinó cómo las modificaciones geométricas influyen en la distribución de campo eléctrico y la temperatura. En particular se analizaron configuraciones con postes elípticos intercalados, los cuales concentran el campo en áreas específicas, reduciendo los efectos térmicos deseados. Las simulaciones iniciales emplearon un voltaje de referencia de 2500 V [8], mientras que el diseño optimizado permitió operar únicamente con 1500 V.

Este estudio demuestra cómo la combinación de diseños geométricos estratégicos y el modelado computacional pueden abordar desafíos propios de la tecnología microfluídica. Al controlar de manera eficaz el calentamiento por efecto Joule y optimizar la concentración de campo eléctrico, se facilita el desarrollo de dispositivos más eficientes y confiables, cuyas aplicaciones potenciales abarcan una amplia variedad de áreas e industrias.

Marco Teórico

Efecto Joule en Sistemas Microfluídicos

En un sistema iEK, el efecto Joule describe la generación de calor al aplicar un campo eléctrico en un medio conductor. Este campo induce un flujo de corriente que genera calor proporcional al cuadrado de la intensidad del campo eléctrico . Este fenómeno, además de provocar fuerzas dielectrofóricas eleva la temperatura del medio, lo que puede impacta la eficiencia de la separación de partículas.

Campo Eléctrico en Sistemas Microfluídicos

En un sistema iEK se introducen obstáculos no conductores en el canal. El campo eléctrico se genera al aplicar una diferencia de potencial entre dos electrodos ubicados en los extremos del microcanal. Estos postes alteran la distribución del campo eléctrico en el fluido, lo que genera zonas de baja y alta intensidad de campo. El campo eléctrico en cualquier punto del canal está relacionada con el potencial eléctrico de la siguiente manera . Donde representa el gradiente del potencial eléctrico.

La presencia de postes genera concentraciones del campo eléctrico en regiones específicas alrededor de los bordes de estas estructuras. Estas concentraciones son zonas de alta intensidad de campo, mientras que en regiones alejadas de los postes, el campo tiende a ser más uniforme. Este comportamiento puede cuantificarse utilizando el gradiente cuadrático del campo eléctrico, (), que describe cómo varía la intensidad del campo en función de la geometría del sistema y permite identificar las zonas de mayor perturbación. En estas zonas de mayor variación del campo eléctrico se concentra el calentamiento por el efecto Joule, impactando directamente la distribución de calor.

Cuando un campo eléctrico se aplica a un fluido conductor, las cargas dentro del fluido comienzan a moverse, generando una corriente eléctrica expresada como:

(1)

donde es la densidad de corriente, la cual es directamente proporcional al producto de la conductividad eléctrica del fluido y el campo eléctrico . La interacción de la corriente eléctrica con el campo provoca que la energía se disipe en forma de calor.

Transferencia de Calor

La densidad de potencia generada en este proceso está dada por la siguiente ecuación:

(2)

donde es la densidad de potencia generada por el efecto Joule, es la conductividad eléctrica del fluido y es la magnitud al cuadrado del campo eléctrico. Esta relación implica que en las zonas de alta intensidad de campo eléctrico, cerca de los postes, la generación de calor será mayor. Este calor se transfiere al fluido de los alrededores, generando gradientes térmicos.

El flujo de calor resultante en el sistema está descrito por la ecuación de transferencia de calor:

(3)

donde es la densidad del fluido, es la capacidad calorífica específica, la cual mide la energía necesaria para aumentar la temperatura del fluido por unidad de masa y describe el movimiento de la energía en forma de calor debido a gradientes de temperatura . El término es la conductividad térmica, mide la capacidad de un material para transferir calor.

Cuando se define una condición de frontera específica para la transferencia de calor, se utiliza la ecuación:

(4)

donde es el vector normal a la superficie de la frontera, este define la dirección perpendicular al límite donde se aplica la condición. Así mismo, es el vector de flujo de calor, es el coeficiente de transferencia de calor por convección y es la temperatura del ambiente. Si , no hay flujo de calor que cruce la superficie.

Amplificación y Resistencia Total

Entre las diferentes maneras que se puede modificar un microcanal para incrementar el campo eléctrico, se toma en cuenta la morfología de los postes en este caso se toma en cuenta un factor de amplificación () el cual depende de un factor escalable () el cual se basa en la relación entre la separación de los postes y el tamaño de la figura de los mismos según su morfología. En el caso de la morfología triangular que se busca replicar en este trabajo; su factor de escalable () y factor de amplificación () se definen de la siguiente manera:

(5)

(6)

donde corresponde a la separación entre postes y siendo la base del triángulo, este valor luego sirve para determinar el valor del factor de amplificación para el campo eléctrico. [7]

Por otro lado, es importante poder llegar a obtener a la misma magnitud e intensidad del campo eléctrico pero modificando el voltaje, donde la cantidad de voltaje requerida para lograr dicho objetivo en la magnitud del campo eléctrico depende de la resistencia total del sistema () que se relaciona con el número de postes en el micro canal dicha ecuación se representa de la siguiente manera. [9]

(7)

donde es la resistencia del medio, es la resistencia de los postes y es el número de postes.

Materiales y Métodos

Para el desarrollo del nuevo canal microfluídico se basó principalmente en la optimización de un canal previamente hecho y reportado en la literatura usando el software de COMSOL Multiphysics, el modelo referencia es de un arreglo de elipses sub optimizados [1,2] para obtener magnitudes de campo eléctrico y temperaturas óptimas modificando el gradiente del campo eléctrico y usando un voltaje inicial para su funcionamiento. En el caso de esta propuesta se usó la misma tabla de parámetros de condiciones iniciales y de materiales, a excepción del voltaje inicial el cual se redujo sin perjudicar las magnitudes. A continuación se presenta en la tabla 1 los parámetros tanto de materiales como de condiciones iniciales que se usaron dentro del modelo de referencia y en la propuesta de modelo.

Propiedad

Valor

Capacidad térmica a presión constante (PDMS)

1460

Permitividad Relativa (PDMS)

2.5

Densidad (PDMS)

970

Conductividad Térmica (PDMS)

0.16

Conductividad Eléctrica (PDMS)

2.15 E-15

Potencial Zeta (PDMS)

-66.7

Permitividad del Medio (Agua)

80

Conductividad Eléctrica Inicial del Medio (Agua)

0.002

Voltaje de Estimulación (Modelo Referencia)

2500

Voltaje de Estimulación (Propuesta de Modelo)

1500

Temperatura Inicial

25°C

Coeficiente de Transferencia de Calor

10

3.1 Parámetros Geométricos y Modelo de Propuesta

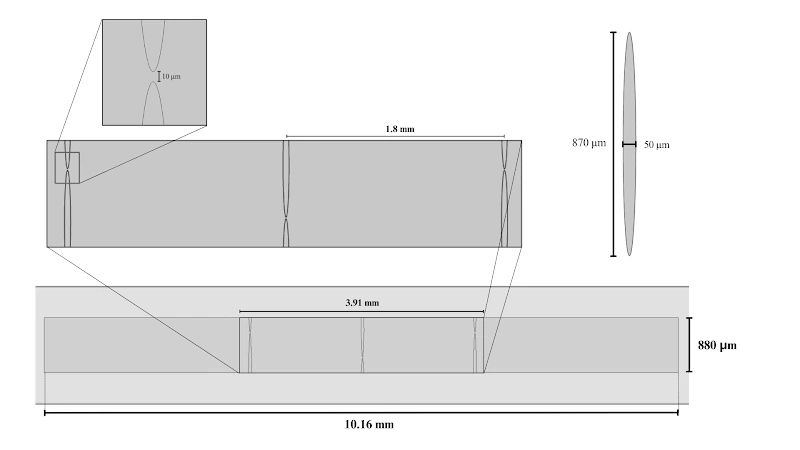
Por otro lado, en cuanto la geometría del canal, en la figura 1 se encuentra un esquema a detalle de las dimensiones del canal, sensor, postes, distancias entre ellos, entre otras propiedades para construirlo en el software de COMSOL Multiphysics. Se trata de un canal microfluídico de 7 de alto, 10.16 de largo y 880 de ancho, donde dentro cuenta con un sensor más pequeño donde se encuentra el arreglo de postes en forma de elipses hechos de PDMS respetando las limitaciones de manufactura y resolución al momento del desarrollo experimental del canal.

El arreglo de postes está caracterizado por permitir una sola entrada y estar acomodados de forma intercalada, el arreglo como tal consta de un arreglo de 3 columnas y 2 filas de elipses cuyas separaciones entre ellos ya se encuentran señaladas en la figura 1, cabe recalcar que la ubicación del espacio entre postes es determinado en función del centro del sensor. Esto se refiere a que el espacio entre postes de la columna 1 y 3 se encuentra 200 por encima del centro del sensor mientras que la columna 2 se encuentra 200 por debajo del centro del sensor.

Resultados y discusiones

El diseño del canal microfluídico con un arreglo intercalado de postes con una sola entrada y salida permitió explorar cómo la geometría del sistema influye en la distribución del campo eléctrico y en la generación de calor por efecto Joule en el sistema. Las simulaciones realizadas demostraron que modificar el diseño de la geometría de postes tiene un impacto significativo en la concentración del campo eléctrico y en la mitigación de efectos térmicos asociados al calentamiento del fluido en el canal.

Figura 2. Simulaciones en COMSOL del modelo de referencia después de 90 segundos usando un voltaje de 2500 V. (A) Intensidad del campo eléctrico , (B) magnitud del logaritmo (), (C) Temperatura después de 90 s. (D) Ilustración del cutline usado para evaluar las predicciones en esta figura.

Estimación del campo eléctrico

Uno de los principales resultados fue la capacidad del sistema para concentrar el campo eléctrico en regiones específicas del canal. Este comportamiento fue favorecido por la disposición intercalada de postes y su geometría elíptica con un semieje mayor mucho más grande que el semieje menor. Como se observa en la Figura 2, las simulaciones del modelo de referencia, después de 90 segundos y aplicando un voltaje de 2500 V, muestran una distribución del campo eléctrico que se concentra alrededor de los postes intercalados. La intensidad del campo eléctrico alcanza sus valores máximos en estas regiones, lo que también coincide con un aumento localizado en la generación de calor debido al efecto Joule. Esto se evidencia en el gradiente cuadrático del campo eléctrico representado en la Figura 2B, el cual resalta las zonas de mayor variación del campo. En la Figura 3, se muestran los resultados del diseño optimizado, donde se aplicó un voltaje reducido de 1500 V. Aquí, se puede apreciar una mayor focalización del campo eléctrico, alcanzando una intensidad de , en comparación con los del modelo de referencia. Este incremento en la intensidad del campo, a pesar del menor voltaje aplicado, demuestra la eficacia del diseño optimizado para concentrar el campo en las regiones específicas.

Figura 3. Simulaciones en COMSOL del modelo propuesto después de 90 segundos usando un voltaje de 1500 V. (1.A) Intensidad del campo eléctrico en el PL1, (2.A) Intensidad del campo eléctrico en el PL2 (B) Temperatura después de 90 s, (1.C) Ilustración del cutline superior usado para evaluar las predicciones en esta figura. (2.C) Ilustración del cutline inferior usado para evaluar las predicciones en esta figura.

Estimación de la temperatura

La temperatura, representada en la Figura 3 C, muestra una notable en el diseño optimizado, pasando de una temperatura inicial de 36ºC a 35ºC después de 90 segundos. Esto se atribuye a una mejor gestión térmica del sistema, producto de la concentración del campo eléctrico en áreas específicas y la reducción del voltaje aplicado. La disminución del calentamiento por efecto Joule refleja la capacidad del diseño para mitigar gradientes térmicos no deseados, garantizando así un desempeño más estable y eficiente del sistema.

Se ilustra cómo la distribución espacial del campo eléctrico y del calor generado está directamente relacionada con las variaciones en el diseño geométrico de los postes. Las simulaciones revelaron que las áreas más cercanas a los postes mostraron una mayor concentración de , mientras que las regiones periféricas mantuvieron temperaturas más bajas y distribuciones de campo menos intensas.

Conclusiones

A partir de lo visto en este trabajo podemos concluir los factores que alteran directamente las propiedades del canal microfluídico con un arreglo de postes intercalados y de una sola entrada. Al modificar el arreglo al de una sola salida entre 2 postes, intercalado y de pocas columnas se fuerza al campo eléctrico a concentrarse en una sola región, lo que genera su incremento en magnitud, evita el incremento de efectos no deseados (Joule heating) y permite bajar significativamente el voltaje necesario; el cambio en la morfología de postes usando elipses con un semieje mayor significativamente más grande que su semieje menor lleva a la una forma en donde deja de comportarse como una elipse para adoptar la forma y comportamiento de una figura triangular donde se puede modificar la base del semi-elipse para modificar el factor de amplificación () y poder focalizar el campo eléctrico al tener figuras más puntiagudas que perturban a mayor magnitud la uniformidad del campo incrementando su intensidad de campo ; igualmente la reducción de cantidad de postes reduce la resistencia total del sistema lo que deriva en la reducción de voltaje necesario para el funcionamiento del sistema debido a la relación entre el número de postes y la resistencia total (). De esta manera se puede es que se pudo identificar ciertas propiedades que se pueden modificar dentro del canal para poder reducir el voltaje y seguir teniendo magnitudes similares a los del modelo inicial.

Conflicto de Interés

Los autores no declaran ningún conflicto de intereses

References

[1] Martins JP, Torrieri G, Santos HA. The importance of microfluidics for the preparation of nanoparticles as advanced drug delivery systems. Expert Opinion On Drug Delivery [Internet]. 6 de marzo de 2018;15(5):469-79. Disponible en: https://doi.org/10.1080/17425247.2018.1446936

[2] Steffen Hardt, Friedhelm Schönfeld. Microfluidic technologies for miniaturized analysis systems [Internet]. Springer; 2007. Disponible en: https://books.google.com.mx/books?hl=en&lr=&id=wHweGP8uQeIC&oi=fnd&pg=PR19&dq=Microfluidic+technologies+for+miniaturized+analysis+systems&ots=ae36Vqm3Pu&sig=v-f07tW_hYKJJG7I8zErF7Kxqn0#v=onepage&q=Microfluidic%20technologies%20for%20miniaturized%20analysis%20systems&f=false

[3] Henrik Bruus. Theoretical microfluidics [Internet]. Copenhague, Dinamarca; 2006. Disponible en: https://homes.nano.aau.dk/lg/Lab-on-Chip2008_files/HenrikBruus_Microfluidics%20lectures.pdf

[4] Ahamed NNN, Mendiola-Escobedo CA, Perez-Gonzalez VH, Lapizco-Encinas BH. Assessing the Discriminatory Capabilities of iEK Devices under DC and DC-Biased AC Stimulation Potentials. Micromachines [Internet]. 14 de diciembre de 2023;14(12):2239. Disponible en: https://doi.org/10.3390/mi14122239

[5] Cetin B, Li D. Effect of Joule heating on electrokinetic transport. Electrophoresis [Internet]. 13 de febrero de 2008;29(5):994-1005. Disponible en: https://doi.org/10.1002/elps.200700601

[6] Xuan X. Joule heating in electrokinetic flow. Electrophoresis [Internet]. 30 de noviembre de 2007;29(1):33-43. Disponible en: https://doi.org/10.1002/elps.200700302

[7] Ruz-Cuen R, De los Santos-Ramírez JM, Cardenas-Benitez B, Ramírez-Murillo CJ, Miller A, Hakim K, et al. Amplification factor in DC insulator-based electrokinetic devices: a theoretical, numerical, and experimental approach to operation voltage reduction for particle trapping. Lab On A Chip [Internet]. 1 de enero de 2021;21(23):4596-607. Disponible en: https://doi.org/10.1039/d1lc00614b

[8] Gallo‐Villanueva RC, Perez‐Gonzalez VH, Cardenas‐Benitez B, Jind B, Martinez‐Chapa SO, Lapizco‐Encinas BH. Joule heating effects in optimized insulator‐based dielectrophoretic devices: An interplay between post geometry and temperature rise. Electrophoresis [Internet]. 18 de marzo de 2019;40(10):1408-16. Disponible en: https://doi.org/10.1002/elps.201800490

[9] Perez-Gonzalez VH, Gallo-Villanueva RC, Cardenas-Benitez B, Martinez-Chapa SO, Lapizco-Encinas BH. Simple Approach to Reducing Particle Trapping Voltage in Insulator-Based Dielectrophoretic Systems. Analytical Chemistry [Internet]. 12 de marzo de 2018;90(7):4310-5. Disponible en: https://doi.org/10.1021/acs.analchem.8b00139

Información Adicional

Archivo de información adicional: https://docs.google.com/document/d/1GKDkZPbnkyySyrr302E12_632firg_5Hu09BlLmBEXM/edit?usp=sharing