Research Data Analysis and Visualization
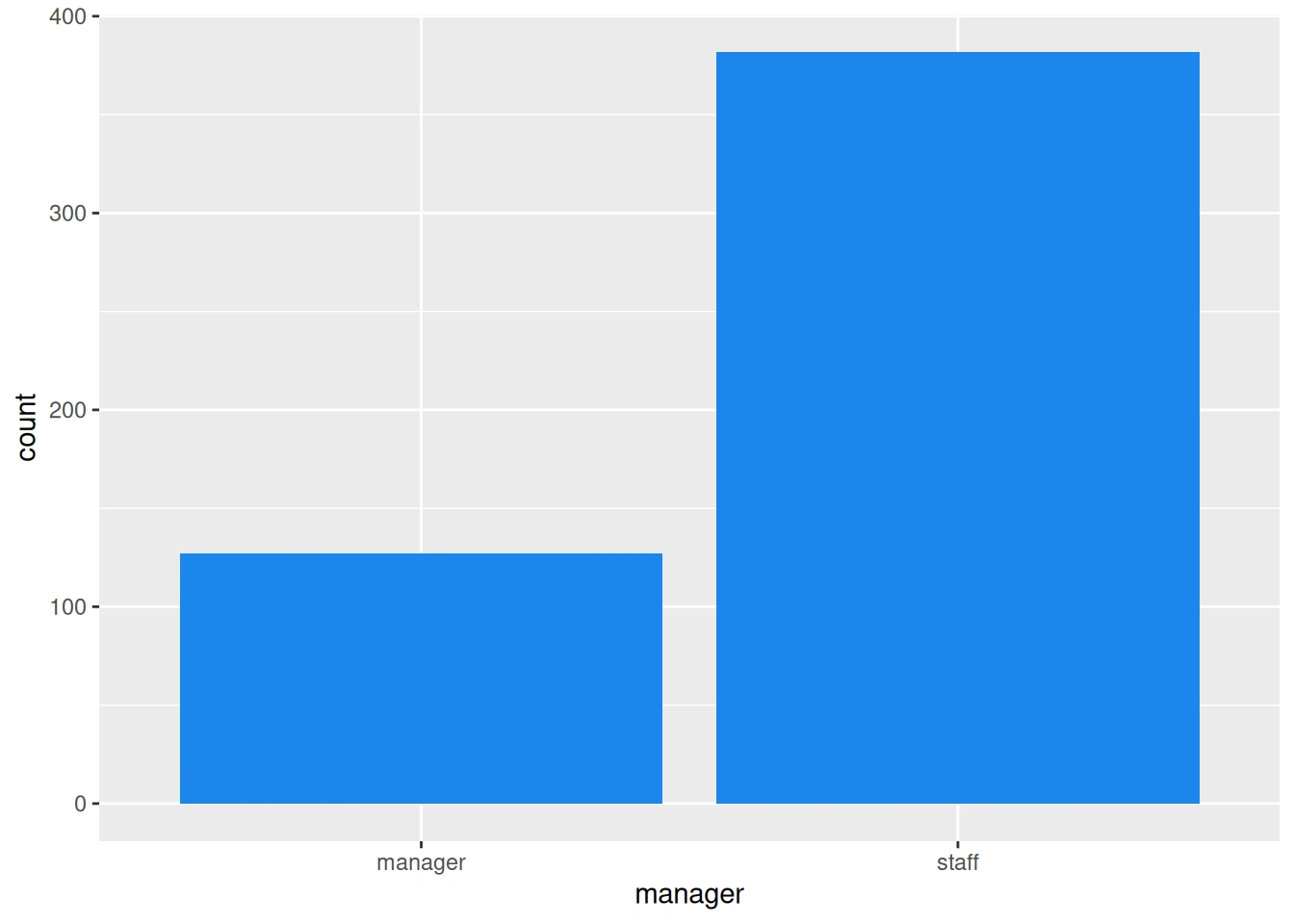
Table of contents
Author
Importing Data
Data was imported from spss file james.sav which was provided by Dr. Dellaneve:
library(tidyverse)
library(haven)
df <- read_spss("data/james.sav")
Selecting Required Data
Some of the columns was omitted from dataset and a report from current variables and their frequency created as a PDF file and the data saved as a new data file:
#Removing Unnecessary Columns from Dataset (Tidying Dataset)
df <- df |>
select(13:210) |>
relocate(ID, 1) |>
arrange(ID) |>
relocate(q2z, q3z, q5z, .after = scale8)
#View the Cleaned Dataset:
sjPlot::view_df(df, show.frq = TRUE)
#Save Cleaned Data
saveRDS(df, "data/clean.rds")
Creating Categorical Variables
In this step, the categorical variables such as gender, race, education, etc. was created from related questions:
library(tidyverse)
library(sjlabelled)
library(sjPlot)
## Reading Clean Dataset:
df <- readRDS("data/clean.rds")
### Changing Management Status (Q136) to Categorical (manager)
df |>
count(Q136)
df <- df |>
mutate(manager = factor (case_when(
Q136 == 1 ~ "manager",
Q136 == 2 ~ "staff"
))) |>
relocate(manager, .after = Q136)
### Changing Q2 to Gender (Factor = categorical)
df <- df |>
mutate(gender = factor (case_when(Q2==1~"male",
Q2==2~"female",
Q2>2~NA))) |>
relocate(gender, .after = Q2)
### Changing Q1 to Categorical Generation
df <- df |>
mutate(generation = factor(case_when(Q1==1~"BabyBoomers",
Q1==2~"GenX",
Q1==3~"GenY",
Q1==4~"GenZ"
))) |>
relocate(generation, .after = Q1)
## Changing Q3 to Categorical Race
df$race <- as_label(df$Q3, keep.labels = TRUE)
df <- df |>
relocate(race, .after = Q3)
## Changing State to Categorical
df$states <- as_label(df$State, keep.labels = TRUE)
df <- df |>
relocate(states, .after = State)
## Changing Q4 to Categorical Education
df$education <- as_label(df$Q4, keep.labels = TRUE)
df <- df |>
relocate(education, .after = Q4)
## Change Q5 (Employment Status) to Categorical empstat
df$empstat <- as_label(df$Q5, keep.labels = TRUE)
df <- df |>
relocate(empstat, .after = Q5)
## Changing Q6 to Categorical Industry
df$industry <- as_label(df$Q6, keep.labels = TRUE)
df <- df |>
relocate(industry, .after = Q6)
## Save Transformed Clean Ready for Analysis Dataset
saveRDS(df, "data/transformd.rds")
Computing Continuous Variables
In this step, continuous (dependent) variables was calculated (took mean):
##Computing Variables of the Study as a New Pivot Table
library(tidyverse)
library(haven)
df <- readRDS("data/transformd.rds")
##Anxiety
df <- df |>
mutate(anxiety = round ((Q10 + Q13 + Q14 + Q15 + Q18 + Q19 + Q20)/7, 2),
.after = Q20)
##Avoidance
##1st Step: Reversing Questions 11, 8, 16, 17
df <- df |>
mutate(Q11New = 6 - Q11, .after = Q11) |>
mutate(Q8New = 6 - Q8, .after = Q8) |>
mutate(Q16New = 6 - Q16, .after = Q16) |>
mutate(Q17New = 6 - Q17, .after = Q17)
##2nd Step: Computing Avoidance from Revised Questions
df <- df |>
mutate(avoidance = round((Q9 + Q12 + Q8New + Q11New + Q16New + Q17New)/6, 2),
.after = Q17New)
##Interpersonal Deviance
##1st Step: Revised Q21
df <- df |>
mutate(Q21New = 6 - Q21, .after = Q21)
##2nd Step: Interpersonal Deviance Variable
df <- df |>
mutate(intpersdev = round((rowSums(across(Q21New:Q27)))/7, 2), .after = Q27)
##Organizational Deviance
df <- df |>
mutate(orgdev = round((rowSums(across(Q28:Q39)))/12, 2), .after = Q39)
##ACE
##1st Step: Reversing Q40-Q44 and Setting Missing Values(NA) for DK/DA values
df <- df |>
mutate(Q40New = case_when(Q40 == 1 ~ 2, Q40 == 2 ~1, Q40 == 3~0,
Q40 == 4~0), .after = Q40)
df <- df |>
mutate(Q41New = case_when(Q41 == 1 ~ 2, Q41 == 2 ~1, Q41 == 3~0,
Q41 == 4~0), .after = Q41)
df <- df |>
mutate(Q42New = case_when(Q42 == 1 ~ 2, Q42 == 2 ~1, Q42 == 3~0,
Q42 == 4~0), .after = Q42)
df <- df |>
mutate(Q43New = case_when(Q43 == 1 ~ 2, Q43 == 2 ~1, Q43 == 3~0,
Q43 == 4~0), .after = Q43)
df <- df |>
mutate(Q44New = case_when(Q44 == 1 ~ 2, Q44 == 2 ~1, Q44 == 3~0,
Q44 == 4~0), .after = Q44)
#2nd Step: Q45-Q50 Missing Values (NA) for DK/DA
df <- df |>
mutate(Q45New = case_when(Q45 == 1 ~ 1, Q45 == 2 ~2, Q45 == 3~3,
Q45 == 4~0, Q45 == 5~0), .after = Q45)
df <- df |>
mutate(Q46New = case_when(Q46 == 1 ~ 1, Q46 == 2 ~2, Q46 == 3~3,
Q46 == 4~0, Q46 == 5~0), .after = Q46)
df <- df |>
mutate(Q47New = case_when(Q47 == 1 ~ 1, Q47 == 2 ~2, Q47 == 3~3,
Q47 == 4~0, Q47 == 5~0), .after = Q47)
df <- df |>
mutate(Q48New = case_when(Q48 == 1 ~ 1, Q48 == 2 ~2, Q48 == 3~3,
Q48 == 4~0, Q48 == 5~0), .after = Q48)
df <- df |>
mutate(Q50New = case_when(Q50 == 1 ~ 1, Q50 == 2 ~2, Q50 == 3~3,
Q50 == 4~0, Q50 == 5~0), .after = Q50)
#3rd Step: Compute ACE from New Revised Questions
df <- df |>
mutate(ace = round((Q40New + Q41New + Q42New + Q43New + Q44New + Q45New
+Q46New + Q47New + Q48New + Q50New), 2), .after = Q50New)
##Phubbing
df <- df |>
mutate(phubbing = round((Q51 + Q52)/2, 2), .after = Q52)
#Employee Engagement
df <- df |>
mutate(empengage = round((rowSums(across(Q60:Q100)))/41, 2), .after = Q100)
#Self-Attachment
##1st Step: Reversing Questions 102, 103, 104, 106, 107, 111
df <- df |>
mutate(Q102New = 6 - Q102, .after = Q102) |>
mutate(Q103New = 6 - Q103, .after = Q103) |>
mutate(Q104New = 6 - Q104, .after = Q104) |>
mutate(Q106New = 6 - Q106, .after = Q106) |>
mutate(Q107New = 6 - Q107, .after = Q107) |>
mutate(Q111New = 6 - Q111, .after = Q111)
##2nd Step: Computing Self-Attachment
df <- df |>
mutate(selfattach = (Q101 + Q102New + Q103New + Q104New + Q105 + Q106New +
Q107New + Q109 + Q111New + Q112)/10, .after = Q112)
#Remote
df <- df |>
mutate(remote = round((Q118 + Q119 + Q120)/3, 2), .after = Q120)
#Focus
df <- df |>
mutate(focus = (Q134 + Q135),
.after = Q135)
#Save File in CSV
write_csv(df, "data/variables.csv")
Categorical Visualization
Management Status Bar Chart:
Gender Bar Charts:
Generation
Race
States
Education
Employment Status
Industries
Spearman Correlations
In this step the Spearman correlations between questions of the study is created:
Anxiety Items
Avoidance Items
Interpersonal Deviance Items
ACE Items
Self-Attachment Items
All Items (Q08 to Q112)
Scatter Plots
Anxiety vs. Avoidance
Interpersonal Deviance vs. Anxiety
Interpersonal Deviance vs. Avodiance
Organizational Deviance vs. Avoidance
OrgDev vs. Anxiety
Test of Normality
Employee Engagement
Shapiro-Wilk normality test
data: df$empengage
W = 1, p-value = 8e-09
Self-Attachment
Shapiro-Wilk normality test
data: df$selfattach
W = 1, p-value = 2e-04
Phubbing
Shapiro-Wilk normality test
data: df$phubbing
W = 0.8, p-value <2e-16
Remote Teams
Shapiro-Wilk normality test
data: df$remote
W = 0.9, p-value = 9e-13
Focus
Shapiro-Wilk normality test
data: df$focus
W = 0.7, p-value <2e-16
Anxiety
Shapiro-Wilk normality test
data: df$anxiety
W = 1, p-value = 1e-10
Avoidance
Shapiro-Wilk normality test
data: df$avoidance
W = 1, p-value = 3e-04
Interpersonal Deviance
Shapiro-Wilk normality test
data: df$intpersdev
W = 0.7, p-value <2e-16
Organizational Deviance
Shapiro-Wilk normality test
data: df$orgdev
W = 0.8, p-value <2e-16
ACE
Shapiro-Wilk normality test
data: df$ace
W = 0.9, p-value = 1e-15
Kruskal Wallis Test
Since our continuous variables are not normally distributed, we used non-parametric test of Kruskal Wallis to find how the variables diverse among demographics:
Employee Engagement Vs. Demographics
As we see in the following results there is not any significant difference regarding employee engagement among demographics:
Asymptotic Kruskal-Wallis Test
data: empengage by
race (American Indian/Native American or Alaska Native, Asian, Black or African American, Native Hawaiian or Other Pacific Islander, Other, Prefer not to say, White or Caucasian)
chi-squared = 10, df = 6, p-value = 0.1
Asymptotic Kruskal-Wallis Test
data: empengage by
education (Associates or technical degree, Bachelor’s degree, Graduate Degree, High school diploma or GED, Some college, but no degree, Less than HS)
chi-squared = 5, df = 5, p-value = 0.5
Asymptotic Kruskal-Wallis Test
data: empengage by
generation (BabyBoomers, GenX, GenY, GenZ)
chi-squared = 5, df = 3, p-value = 0.2
Asymptotic Kruskal-Wallis Test
data: empengage by gender (female, male)
chi-squared = 0.04, df = 1, p-value = 0.8
Self-Attachment Vs. Demographics
As the following results show, the self-attachment difference is significant for education and generation at p = 0.05
Asymptotic Kruskal-Wallis Test
data: selfattach by
race (American Indian/Native American or Alaska Native, Asian, Black or African American, Native Hawaiian or Other Pacific Islander, Other, Prefer not to say, White or Caucasian)
chi-squared = 6, df = 6, p-value = 0.5
Asymptotic Kruskal-Wallis Test
data: selfattach by
education (Associates or technical degree, Bachelor’s degree, Graduate Degree, High school diploma or GED, Some college, but no degree, Less than HS)
chi-squared = 19, df = 5, p-value = 0.002
Asymptotic Kruskal-Wallis Test
data: selfattach by
generation (BabyBoomers, GenX, GenY, GenZ)
chi-squared = 55, df = 3, p-value = 6e-12
Asymptotic Kruskal-Wallis Test
data: selfattach by gender (female, male)
chi-squared = 4, df = 1, p-value = 0.05
Phubbing
The results below show that phubbing has a significant difference in generation.
Asymptotic Kruskal-Wallis Test
data: phubbing by
race (American Indian/Native American or Alaska Native, Asian, Black or African American, Native Hawaiian or Other Pacific Islander, Other, Prefer not to say, White or Caucasian)
chi-squared = 3, df = 6, p-value = 0.8
Asymptotic Kruskal-Wallis Test
data: phubbing by
education (Associates or technical degree, Bachelor’s degree, Graduate Degree, High school diploma or GED, Some college, but no degree, Less than HS)
chi-squared = 4, df = 5, p-value = 0.5
Asymptotic Kruskal-Wallis Test
data: phubbing by
generation (BabyBoomers, GenX, GenY, GenZ)
chi-squared = 25, df = 3, p-value = 2e-05
Asymptotic Kruskal-Wallis Test
data: phubbing by gender (female, male)
chi-squared = 2, df = 1, p-value = 0.2
Remote Teams
Results indicate a significant difference for Remote Teams regarding generation
Asymptotic Kruskal-Wallis Test
data: remote by
race (American Indian/Native American or Alaska Native, Asian, Black or African American, Native Hawaiian or Other Pacific Islander, Other, Prefer not to say, White or Caucasian)
chi-squared = 9, df = 6, p-value = 0.2
Asymptotic Kruskal-Wallis Test
data: remote by
education (Associates or technical degree, Bachelor’s degree, Graduate Degree, High school diploma or GED, Some college, but no degree, Less than HS)
chi-squared = 6, df = 5, p-value = 0.3
Asymptotic Kruskal-Wallis Test
data: remote by
generation (BabyBoomers, GenX, GenY, GenZ)
chi-squared = 12, df = 3, p-value = 0.009
Asymptotic Kruskal-Wallis Test
data: remote by gender (female, male)
chi-squared = 0.08, df = 1, p-value = 0.8
Focus
Results indicate focus has a significant difference regarding generation
Asymptotic Kruskal-Wallis Test
data: focus by
race (American Indian/Native American or Alaska Native, Asian, Black or African American, Native Hawaiian or Other Pacific Islander, Other, Prefer not to say, White or Caucasian)
chi-squared = 10, df = 6, p-value = 0.1
Asymptotic Kruskal-Wallis Test
data: focus by
education (Associates or technical degree, Bachelor’s degree, Graduate Degree, High school diploma or GED, Some college, but no degree, Less than HS)
chi-squared = 4, df = 5, p-value = 0.6
Asymptotic Kruskal-Wallis Test
data: focus by
generation (BabyBoomers, GenX, GenY, GenZ)
chi-squared = 28, df = 3, p-value = 3e-06
Asymptotic Kruskal-Wallis Test
data: focus by gender (female, male)
chi-squared = 2, df = 1, p-value = 0.1
Anxiety
Anxiety shows a significant difference in generation and gender
Asymptotic Kruskal-Wallis Test
data: anxiety by
race (American Indian/Native American or Alaska Native, Asian, Black or African American, Native Hawaiian or Other Pacific Islander, Other, Prefer not to say, White or Caucasian)
chi-squared = 5, df = 6, p-value = 0.5
Asymptotic Kruskal-Wallis Test
data: anxiety by
education (Associates or technical degree, Bachelor’s degree, Graduate Degree, High school diploma or GED, Some college, but no degree, Less than HS)
chi-squared = 6, df = 5, p-value = 0.3
Asymptotic Kruskal-Wallis Test
data: anxiety by
generation (BabyBoomers, GenX, GenY, GenZ)
chi-squared = 39, df = 3, p-value = 2e-08
Asymptotic Kruskal-Wallis Test
data: anxiety by gender (female, male)
chi-squared = 5, df = 1, p-value = 0.03
Avoidance
Asymptotic Kruskal-Wallis Test
data: avoidance by
race (American Indian/Native American or Alaska Native, Asian, Black or African American, Native Hawaiian or Other Pacific Islander, Other, Prefer not to say, White or Caucasian)
chi-squared = 6, df = 6, p-value = 0.4
Asymptotic Kruskal-Wallis Test
data: avoidance by
education (Associates or technical degree, Bachelor’s degree, Graduate Degree, High school diploma or GED, Some college, but no degree, Less than HS)
chi-squared = 8, df = 5, p-value = 0.2
Asymptotic Kruskal-Wallis Test
data: avoidance by
generation (BabyBoomers, GenX, GenY, GenZ)
chi-squared = 20, df = 3, p-value = 2e-04
Asymptotic Kruskal-Wallis Test
data: avoidance by gender (female, male)
chi-squared = 0.7, df = 1, p-value = 0.4
Interpersonal Deviance
Asymptotic Kruskal-Wallis Test
data: intpersdev by
race (American Indian/Native American or Alaska Native, Asian, Black or African American, Native Hawaiian or Other Pacific Islander, Other, Prefer not to say, White or Caucasian)
chi-squared = 21, df = 6, p-value = 0.002
Asymptotic Kruskal-Wallis Test
data: intpersdev by
education (Associates or technical degree, Bachelor’s degree, Graduate Degree, High school diploma or GED, Some college, but no degree, Less than HS)
chi-squared = 10, df = 5, p-value = 0.08
Asymptotic Kruskal-Wallis Test
data: intpersdev by
generation (BabyBoomers, GenX, GenY, GenZ)
chi-squared = 29, df = 3, p-value = 3e-06
Asymptotic Kruskal-Wallis Test
data: intpersdev by gender (female, male)
chi-squared = 10, df = 1, p-value = 0.001
Organizational Deviance
Asymptotic Kruskal-Wallis Test
data: orgdev by
race (American Indian/Native American or Alaska Native, Asian, Black or African American, Native Hawaiian or Other Pacific Islander, Other, Prefer not to say, White or Caucasian)
chi-squared = 2, df = 6, p-value = 0.9
Asymptotic Kruskal-Wallis Test
data: orgdev by
education (Associates or technical degree, Bachelor’s degree, Graduate Degree, High school diploma or GED, Some college, but no degree, Less than HS)
chi-squared = 6, df = 5, p-value = 0.3
Asymptotic Kruskal-Wallis Test
data: orgdev by
generation (BabyBoomers, GenX, GenY, GenZ)
chi-squared = 16, df = 3, p-value = 0.001
Asymptotic Kruskal-Wallis Test
data: orgdev by gender (female, male)
chi-squared = 8, df = 1, p-value = 0.006
ACE
Asymptotic Kruskal-Wallis Test
data: ace by
race (American Indian/Native American or Alaska Native, Asian, Black or African American, Native Hawaiian or Other Pacific Islander, Other, Prefer not to say, White or Caucasian)
chi-squared = 8, df = 6, p-value = 0.2
Asymptotic Kruskal-Wallis Test
data: ace by
education (Associates or technical degree, Bachelor’s degree, Graduate Degree, High school diploma or GED, Some college, but no degree, Less than HS)
chi-squared = 20, df = 5, p-value = 0.001
Asymptotic Kruskal-Wallis Test
data: ace by
generation (BabyBoomers, GenX, GenY, GenZ)
chi-squared = 6, df = 3, p-value = 0.1
Asymptotic Kruskal-Wallis Test
data: ace by gender (female, male)
chi-squared = 1, df = 1, p-value = 0.2
Post-Hocs
Interpersonal Deviance vs. Race
dunn.test(df$intpersdev, df$race, method = "bonferroni")
Kruskal-Wallis rank sum test
data: x and group
Kruskal-Wallis chi-squared = 20.9622, df = 6, p-value = 0
Comparison of x by group
(Bonferroni)
Col Mean-|
Row Mean | American Asian Black or Native H Other Prefer n
---------+------------------------------------------------------------------
Asian | 2.275638
| 0.2401
|
Black or | 0.663769 -3.205398
| 1.0000 0.0142*
|
Native H | -0.822720 -2.382108 -1.355908
| 1.0000 0.1807 1.0000
|
Other | 2.386945 0.394801 3.007857 2.487716
| 0.1784 1.0000 0.0276 0.1350
|
Prefer n | 0.557103 -1.208623 0.151427 1.196141 -1.372575
| 1.0000 1.0000 1.0000 1.0000 1.0000
|
White or | 1.268746 -2.424650 1.587176 1.728215 -2.328179 0.314108
| 1.0000 0.1609 1.0000 0.8815 0.2090 1.0000
alpha = 0.05
Reject Ho if p <= alpha/2
Interpersonal Deviance vs. Generation
dunn.test(df$intpersdev, df$generation, method = "bonferroni")
Kruskal-Wallis rank sum test
data: x and group
Kruskal-Wallis chi-squared = 28.6773, df = 3, p-value = 0
Comparison of x by group
(Bonferroni)
Col Mean-|
Row Mean | BabyBoom GenX GenY
---------+---------------------------------
GenX | -0.768167
| 1.0000
|
GenY | -3.420578 -2.640559
| 0.0019* 0.0248*
|
GenZ | -4.650167 -3.870110 -1.247611
| 0.0000* 0.0003* 0.6365
alpha = 0.05
Reject Ho if p <= alpha/2
Organizational Deviance vs Generation
dunn.test(df$orgdev, df$generation, method = "bonferroni")
Kruskal-Wallis rank sum test
data: x and group
Kruskal-Wallis chi-squared = 15.6705, df = 3, p-value = 0
Comparison of x by group
(Bonferroni)
Col Mean-|
Row Mean | BabyBoom GenX GenY
---------+---------------------------------
GenX | -0.359073
| 1.0000
|
GenY | -3.451875 -3.080037
| 0.0017* 0.0062*
|
GenZ | -2.201194 -1.836456 1.227717
| 0.0832 0.1989 0.6587
alpha = 0.05
Reject Ho if p <= alpha/2
ACE vs. Education
dunn.test(df$ace, df$education, method = "bonferroni")
Kruskal-Wallis rank sum test
data: x and group
Kruskal-Wallis chi-squared = 20.266, df = 5, p-value = 0
Comparison of x by group
(Bonferroni)
Col Mean-|
Row Mean | Associat Bachelor Graduate High sch Less tha
---------+-------------------------------------------------------
Bachelor | 0.933954
| 1.0000
|
Graduate | 2.520125 1.948237
| 0.0880 0.3854
|
High sch | 0.383112 -0.568113 -2.300443
| 1.0000 1.0000 0.1607
|
Less tha | -0.528918 -0.825682 -1.398067 -0.659302
| 1.0000 1.0000 1.0000 1.0000
|
Some col | -1.636658 -2.914011 -4.331049 -2.164880 -0.012443
| 0.7628 0.0268 0.0001* 0.2280 1.0000
alpha = 0.05
Reject Ho if p <= alpha/2
Avoidance vs. Generation
dunn.test(df$avoidance, df$generation, method = "bonferroni")
Kruskal-Wallis rank sum test
data: x and group
Kruskal-Wallis chi-squared = 19.5935, df = 3, p-value = 0
Comparison of x by group
(Bonferroni)
Col Mean-|
Row Mean | BabyBoom GenX GenY
---------+---------------------------------
GenX | 2.574562
| 0.0301
|
GenY | 1.733197 -0.843147
| 0.2492 1.0000
|
GenZ | 4.345403 1.774295 2.617525
| 0.0000* 0.2280 0.0266
alpha = 0.05
Reject Ho if p <= alpha/2
Anxiety vs. Generation
dunn.test(df$anxiety, df$generation, method = "bonferroni")
Kruskal-Wallis rank sum test
data: x and group
Kruskal-Wallis chi-squared = 38.8801, df = 3, p-value = 0
Comparison of x by group
(Bonferroni)
Col Mean-|
Row Mean | BabyBoom GenX GenY
---------+---------------------------------
GenX | -0.592811
| 1.0000
|
GenY | -3.214476 -2.610278
| 0.0039* 0.0271
|
GenZ | -5.539950 -4.930446 -2.340168
| 0.0000* 0.0000* 0.0578
alpha = 0.05
Reject Ho if p <= alpha/2
Interpersonal Deviance vs. Gender
dunn.test(df$intpersdev, df$generation, method = "bonferroni")
Kruskal-Wallis rank sum test
data: x and group
Kruskal-Wallis chi-squared = 28.6773, df = 3, p-value = 0
Comparison of x by group
(Bonferroni)
Col Mean-|
Row Mean | BabyBoom GenX GenY
---------+---------------------------------
GenX | -0.768167
| 1.0000
|
GenY | -3.420578 -2.640559
| 0.0019* 0.0248*
|
GenZ | -4.650167 -3.870110 -1.247611
| 0.0000* 0.0003* 0.6365
alpha = 0.05
Reject Ho if p <= alpha/2
Wilcoxon Test
Since Gender has two categories in our study (male and female) we used Wilcoxon test to find out about the difference among groups:
Employee Engagement vs. Gender
wilcox.test(empengage~gender, data = df, na.rm = TRUE)
Wilcoxon rank sum test with continuity correction
data: empengage by gender
W = 31678, p-value = 0.8
alternative hypothesis: true location shift is not equal to 0
Self-Attachment vs. Gender
wilcox_test(selfattach~gender, data = df)
Asymptotic Wilcoxon-Mann-Whitney Test
data: selfattach by gender (female, male)
Z = 2, p-value = 0.05
alternative hypothesis: true mu is not equal to 0
Phubbing vs. Gender
wilcox_test(phubbing~gender, data = df)
Asymptotic Wilcoxon-Mann-Whitney Test
data: phubbing by gender (female, male)
Z = 1, p-value = 0.2
alternative hypothesis: true mu is not equal to 0
Remote vs. Gender
wilcox_test(remote~gender, data = df)
Asymptotic Wilcoxon-Mann-Whitney Test
data: remote by gender (female, male)
Z = 0.3, p-value = 0.8
alternative hypothesis: true mu is not equal to 0
Focus vs. Gender
wilcox_test(focus~gender, data = df)
Asymptotic Wilcoxon-Mann-Whitney Test
data: focus by gender (female, male)
Z = 2, p-value = 0.1
alternative hypothesis: true mu is not equal to 0
Anxiety vs. Gender
wilcox_test(anxiety~gender, data = df)
Asymptotic Wilcoxon-Mann-Whitney Test
data: anxiety by gender (female, male)
Z = -2, p-value = 0.03
alternative hypothesis: true mu is not equal to 0
Avoidance vs. Gender
wilcox_test(avoidance~gender, data = df)
Asymptotic Wilcoxon-Mann-Whitney Test
data: avoidance by gender (female, male)
Z = 0.8, p-value = 0.4
alternative hypothesis: true mu is not equal to 0
Interpersonal Deviance vs. Gender
wilcox_test(intpersdev~gender, data = df)
Asymptotic Wilcoxon-Mann-Whitney Test
data: intpersdev by gender (female, male)
Z = -3, p-value = 0.001
alternative hypothesis: true mu is not equal to 0
Organizational Deviance vs. Gender
wilcox_test(orgdev~gender, data = df)
Asymptotic Wilcoxon-Mann-Whitney Test
data: orgdev by gender (female, male)
Z = -3, p-value = 0.006
alternative hypothesis: true mu is not equal to 0
ACE vs. Gender
wilcox_test(ace~gender, data = df)
Asymptotic Wilcoxon-Mann-Whitney Test
data: ace by gender (female, male)
Z = 1, p-value = 0.2
alternative hypothesis: true mu is not equal to 0
Means Across Demographics
We took mean for variables with a significant difference to see how different categories behave
Interpersonel Deviance vs. Race
# A tibble: 7 × 2
race mean_intpersdev
<fct> <dbl>
1 American Indian/Native American or Alaska Native 1.61
2 Asian 1.21
3 Black or African American 1.49
4 Native Hawaiian or Other Pacific Islander 1.75
5 Other 1.16
6 Prefer not to say 1.35
7 White or Caucasian 1.33
Interpersonal Deviance vs. Generation
# A tibble: 4 × 2
generation mean_intpersdev
<fct> <dbl>
1 BabyBoomers 1.20
2 GenX 1.26
3 GenY 1.43
4 GenZ 1.54
Interpersonal Deviance vs. Gender
# A tibble: 3 × 2
gender mean_intpersdev
<fct> <dbl>
1 female 1.29
2 male 1.42
3 <NA> 1.38
Organizational Deviance vs. Generation
# A tibble: 4 × 2
generation mean_orgdev
<fct> <dbl>
1 BabyBoomers 1.39
2 GenX 1.42
3 GenY 1.63
4 GenZ 1.62
Organizational Deviance vs. Gender
# A tibble: 3 × 2
gender mean_orgdev
<fct> <dbl>
1 female 1.45
2 male 1.58
3 <NA> 1.70
Self-Attachement vs. Education
# A tibble: 6 × 2
education mean_self_attach
<fct> <dbl>
1 Associates or technical degree 3.52
2 Bachelor’s degree 3.61
3 Graduate Degree 3.59
4 High school diploma or GED 3.34
5 Some college, but no degree 3.54
6 Less than HS 3.28
Phubbing vs. Generation
# A tibble: 4 × 2
generation mean_phubbing
<fct> <dbl>
1 BabyBoomers 1.49
2 GenX 1.73
3 GenY 1.91
4 GenZ 1.87
Remote vs. Generation
# A tibble: 4 × 2
generation mean_remote
<fct> <dbl>
1 BabyBoomers 3.41
2 GenX 3.73
3 GenY 3.76
4 GenZ 3.58
Focus vs. Generation
# A tibble: 4 × 2
generation mean_focus
<fct> <dbl>
1 BabyBoomers 3.52
2 GenX 3.51
3 GenY 3.12
4 GenZ 3.18
Anxiety vs. Generation
# A tibble: 4 × 2
generation mean_anxiety
<fct> <dbl>
1 BabyBoomers 1.94
2 GenX 2.01
3 GenY 2.23
4 GenZ 2.47
Anxiety vs. Gender
# A tibble: 3 × 2
gender mean_anxiety
<fct> <dbl>
1 female 2.08
2 male 2.24
3 <NA> 2.38
Avoidance vs. Generation
# A tibble: 4 × 2
generation mean_avoidance
<fct> <dbl>
1 BabyBoomers 3.35
2 GenX 3.08
3 GenY 3.19
4 GenZ 2.91
ACE vs. Education
# A tibble: 6 × 2
education mean_ace
<fct> <dbl>
1 Associates or technical degree 12.8
2 Bachelor’s degree 12.4
3 Graduate Degree 11.8
4 High school diploma or GED 12.7
5 Some college, but no degree 13.7
6 Less than HS 13.8
Like this project
Posted May 25, 2025
Data analysis and visualization for Dr. Dellaneve's research.