Machine Learning Algorithm Series: Kernel Eigenvoices Algorithm

The kernel eigenvoices algorithm is a technique used in speech processing and automatic speech recognition. The goal of the algorithm is to extract a set of “eigenvoices” from a given dataset of speech samples, which can then be used as a basis for a speaker-independent speech recognition system.

The algorithm begins by constructing a kernel matrix, which is a symmetric matrix that encodes the similarity between all pairs of speech samples in the dataset. The kernel matrix is then used to compute the eigenvectors, which are the directions in feature space along which the data varies the most. These eigenvectors are used to define a set of “eigenvoices”, which are linear combinations of the original speech samples.

The eigenvoices can be used as a feature representation for the speech samples and can be used to train a speaker-independent speech recognition system. The eigenvoices are orthogonal to each other and are ranked by their corresponding eigenvalues, which indicate the amount of variation in the data explained by each eigenvoice.

One of the key advantages of the kernel eigenvoices algorithm is that it can be applied to non-linearly separated data, which is common in speech data. This is achieved by using a kernel function, which maps the original data into a higher-dimensional space where it becomes linearly separable. Common kernel functions used in speech processing include the radial basis function (RBF) and the polynomial kernel.

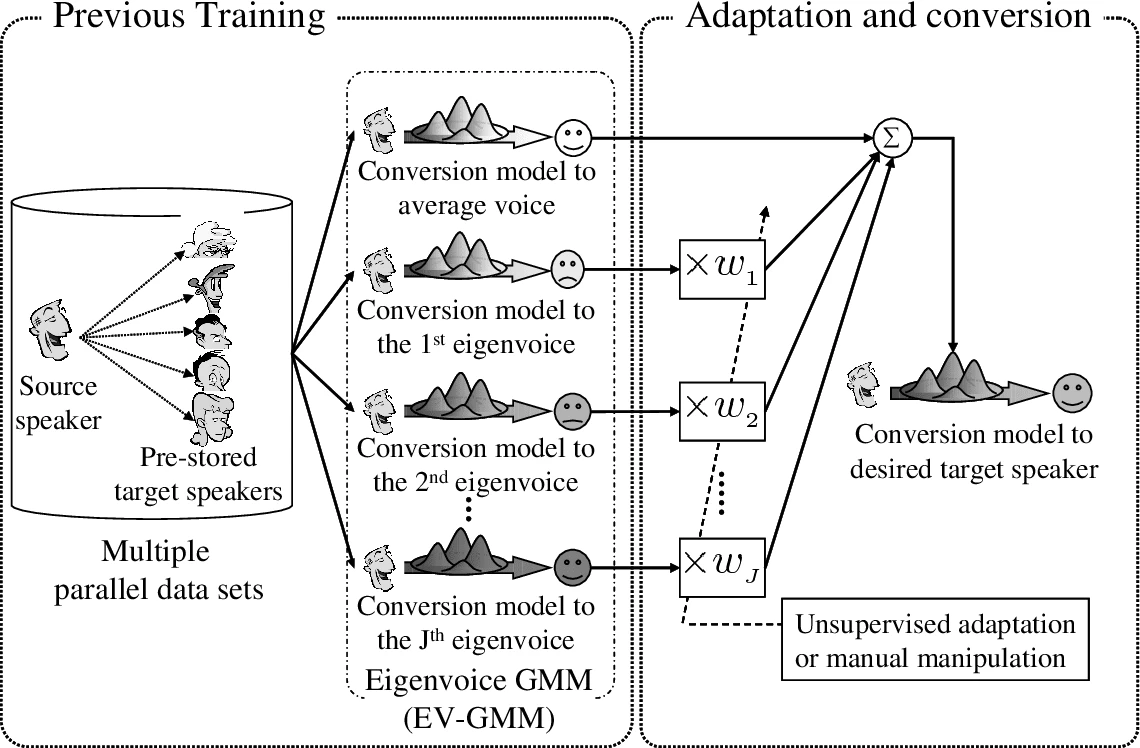
The kernel eigenvoices algorithm can be broken down into several steps:

Data preprocessing: The speech samples are preprocessed to extract features that are relevant for speech recognition. Common feature extraction techniques include Mel-frequency cepstral coefficients (MFCCs), which are widely used in speech processing.

Kernel matrix construction: A kernel matrix is constructed from the feature vectors extracted from the speech samples. The kernel matrix encodes the similarity between all pairs of speech samples in the dataset. The kernel matrix is symmetric and positive semi-definite.

Eigenvalue decomposition: The eigenvectors and eigenvalues of the kernel matrix are computed. The eigenvectors are the directions in feature space along which the data varies the most. These eigenvectors are used to define a set of “eigenvoices”, which are linear combinations of the original speech samples.

Eigenvoice ranking: The eigenvoices are ranked by their corresponding eigenvalues, which indicate the amount of variation in the data explained by each eigenvoice. The eigenvoices with the highest eigenvalues are considered the most important and are used to represent the speech samples.

Training a speaker-independent recognition system: The eigenvoices are used as a representation for the speech samples and can be used to train a speaker-independent speech recognition system. The eigenvoices are orthogonal to each other and provide a compact and efficient representation of the speech data

Another advantage of the kernel eigenvoices algorithm is its ability to capture the underlying structure of the speech data, which can be useful for speech recognition tasks. The algorithm can also be used for speaker verification and speaker identification tasks.

Let’s start coding with Python:

In this example, we first define a kernel function using the radial basis function (RBF) kernel from sklearn.metrics.pairwise module. Then we define the eigenvoices function, which takes a dataset (X) and the number of eigenvoices to extract (n_components) as input. Inside the function, we first compute the kernel matrix using the kernel function and the input dataset. Then we use the PCA class from the sklearn.decomposition module to compute the eigenvectors and eigenvalues of the kernel matrix. Finally, we use the eigenvectors and eigenvalues to compute the eigenvoices, which are returned as the output of the function

Here is an example of how to implement the kernel eigenvoices algorithm in Julia:

This example is similar to the previous one. We first define a kernel function using the RBF kernel. Then we define the eigenvoices function, which takes a dataset (X) and the number of eigenvoices to extract (n_components) as input. Inside the function, we first compute the kernel matrix using the kernel function and input dataset. Then we use the eigenvectors and eigenvalues from the LinearAlgebra package to compute the eigenvoices, which are returned as the output of the function.

The following code is an example of how to implement the kernel eigenvoices algorithm in R. This code uses the kernlab library, which provides a set of kernel functions and tools for kernel-based learning in R.

In this example, the first step is to load the kernlab library. Next, the code loads the speech dataset using read.csv() function. The speech data is assumed to be in a csv file with a header row.

The next step is to extract features from the speech samples. The extractFeatures() function is used for this purpose. This function takes as input the speech data and returns a matrix of feature vectors. The specific features that are extracted will depend on the task at hand and the quality of the data.

Once the features are extracted, the kernel matrix is constructed using the rbfkernel() function. This function takes as input the feature vectors and returns a kernel matrix that encodes the similarity between all pairs of speech samples in the dataset.

The next step is to compute the eigenvectors and eigenvalues of the kernel matrix using the eigen() function. The eigenvectors are used to define a set of eigenvoices, which are linear combinations of the original speech samples.

The eigenvoices are then ranked by their corresponding eigenvalues. The eigenvoices with the highest eigenvalues are considered the most important and are used to represent the speech samples.

Finally, a speaker-independent recognition system is trained using the ranked eigenvoices. The trainSpeechRecognitionModel() function is used to train the model. This function takes as input the ranked eigenvoices and the speaker labels and returns a trained model.

Once the model is trained, it can be tested on new speech samples using the predict() function. The test data is assumed to be in a csv file with a header row and it is passed to the predict function along with the trained model. This will return the predictions for the new speech samples.

It’s worth to note that this example is a simplified version of kernel eigenvoices algorithm and in real-world scenarios, there are many factors such as choosing the right kernel function, parameter tuning, and cross-validation that needs to be considered for optimal results.

For implementing eigenvoices algorithm as it requires a deep understanding of the dataset and the specific requirements of the application. The codes I have provided are just examples and may require modification depending on the specific dataset and application.

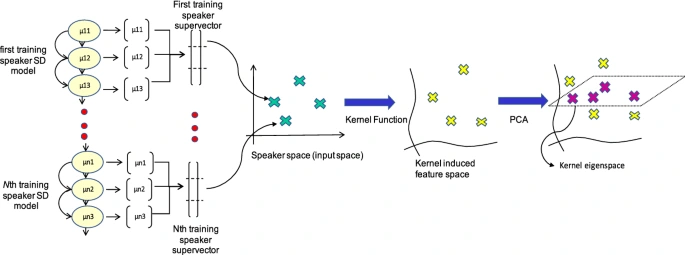
In general, the steps for implementing the kernel eigenvoices algorithm are as follows:

Preprocess the data by extracting relevant features from the speech samples.

Construct a kernel matrix from the feature vectors.

Compute the eigenvectors and eigenvalues of the kernel matrix.

Use the eigenvectors to define a set of “eigenvoices”.

Use the eigenvoices as a feature representation for the speech samples and train a speaker-independent speech recognition system.

To implement this algorithm, you can use libraries like scikit-learn for Python, KernelEigenvoices for or kernlab for R, which provide pre-built functions for kernel PCA and eigenvalue decomposition. You will also need to choose a kernel function that is appropriate for your dataset and tweak the parameters of the algorithm to achieve the best performance.

It is important to have a good understanding of the dataset and the specific requirements of the application in order to implement the kernel eigenvoices algorithm successfully. I suggest consulting with a specialist in the field if you have trouble implementing algorithm.

In conclusion, the kernel eigenvoices algorithm is a powerful technique for extracting a set of “eigenvoices” from given dataset of speech samples, which can then be used as a basis for a speaker-independent speech recognition system. The algorithm is able to handle non-linearly separated data, which is common in speech data, bu using a kernel function to map the data into a higher-dimensional space, where it becomes linearly separable. It captures the underlying structure of the speech data and can be used for speaker verification and speaker identification tasks as well.

Thank you for reading this article! For any suggestions please leave a comment! You can find code examples and more on my Github page!

Website LinkedIn GitHub

Email: info@mertdemir.org